46. Schelling’s Segregation Model #

Contents

Schelling’s Segregation Model
- Overview
- The Model
- Results
- Exercises
- Solutions

46.1. Overview #

In 1969, Thomas C. Schelling developed a simple but striking model of racial segregation [Sch69].

His model studies the dynamics of racially mixed neighborhoods.

Like much of Schelling’s work, the model shows how local interactions can lead to surprising aggregate structure.

In particular, it shows that relatively mild preference for neighbors of similar race can lead in aggregate to the collapse of mixed neighborhoods, and high levels of segregation.

In recognition of this and other research, Schelling was awarded the 2005 Nobel Prize in Economic Sciences (joint with Robert Aumann).

In this lecture we (in fact you) will build and run a version of Schelling’s model.

46.2. The Model #

We will cover a variation of Schelling’s model that is easy to program and captures the main idea.

Suppose we have two types of people: orange people and green people.

For the purpose of this lecture, we will assume there are 250 of each type.

These agents all live on a single unit square.

The location of an agent is just a point \((x, y)\), where \(0 < x, y < 1\).

46.2.1. Preferences#

We will say that an agent is happy if half or more of her 10 nearest neighbors are of the same type.

Here ‘nearest’ is in terms of Euclidean distance.

An agent who is not happy is called unhappy.

An important point here is that agents are not averse to living in mixed areas.

They are perfectly happy if half their neighbors are of the other color.

46.2.2. Behavior#

Initially, agents are mixed together (integrated).

In particular, the initial location of each agent is an independent draw from a bivariate uniform distribution on \(S = (0, 1)^2\).

Now, cycling through the set of all agents, each agent is now given the chance to stay or move.

We assume that each agent will stay put if they are happy and move if unhappy.

The algorithm for moving is as follows

Draw a random location in \(S\)
If happy at new location, move there
Else, go to step 1

In this way, we cycle continuously through the agents, moving as required.

We continue to cycle until no one wishes to move.

46.3. Results #

Let’s have a look at the results we got when we coded and ran this model.

As discussed above, agents are initially mixed randomly together

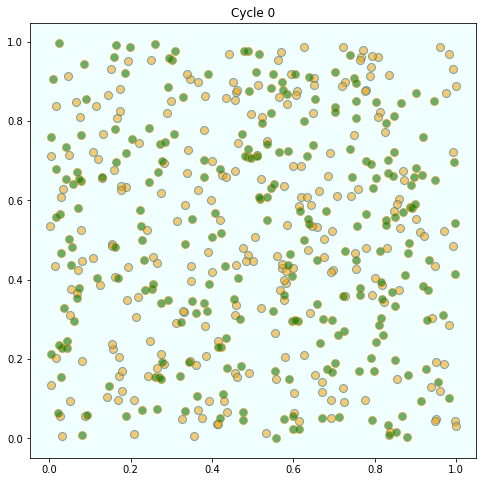
But after several cycles they become segregated into distinct regions

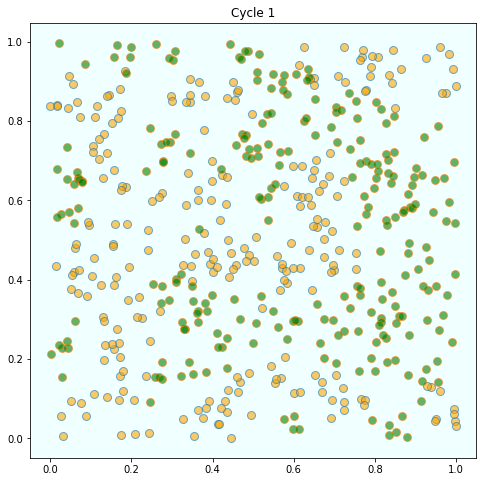
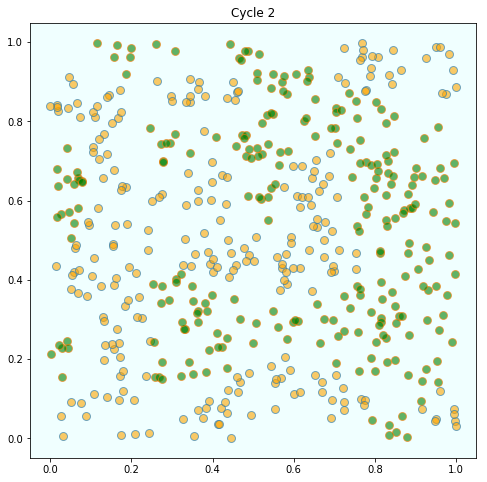
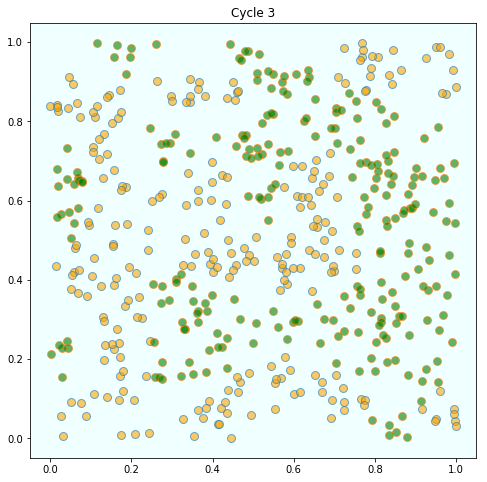
In this instance, the program terminated after 4 cycles through the set of agents, indicating that all agents had reached a state of happiness.

What is striking about the pictures is how rapidly racial integration breaks down.

This is despite the fact that people in the model don’t actually mind living mixed with the other type.

Even with these preferences, the outcome is a high degree of segregation.

46.4. Exercises #

46.4.1. Exercise 1#

Implement and run this simulation for yourself.

Use 250 agents of each type.

46.5. Solutions #

46.5.1. Exercise 1#

Here’s one solution that does the job we want. If you feel like a further exercise you can probably speed up some of the computations and then increase the number of agents.

using Plots, LinearAlgebra, Statistics

Agent(; kind, location = rand(2)) = (; kind, location)

draw_location!(a) = a.location .= rand(2)

# distance is just 2 norm: uses our subtraction function
get_distance(a, agent) = norm(a.location - agent.location)

function is_happy(a)
    distances = [(get_distance(a, agent), agent) for agent in agents]
    sort!(distances)
    neighbors = [agent for (d, agent) in distances[1:neighborhood_size]]
    share = mean(isequal(a.kind), other.kind for other in neighbors)

    # can also do
    # share = mean(isequal(a.kind),
    #              first(agents[idx]) for idx in
    #              partialsortperm(get_distance.(Ref(a), agents),
    #                              1:neighborhood_size))

    return share >= preference
end

function update!(a)
    # If not happy, then randomly choose new locations until happy.
    while !is_happy(a)
        draw_location!(a)
    end
end

function plot_distribution(agents)
    x_vals_0, y_vals_0 = zeros(0), zeros(0)
    x_vals_1, y_vals_1 = zeros(0), zeros(0)

    # obtain locations of each type
    for agent in agents
        x, y = agent.location
        if agent.kind == 0
            push!(x_vals_0, x)
            push!(y_vals_0, y)
        else
            push!(x_vals_1, x)
            push!(y_vals_1, y)
        end
    end

    p = scatter(x_vals_0, y_vals_0, color = :orange, markersize = 8,
                alpha = 0.6)
    scatter!(x_vals_1, y_vals_1, color = :green, markersize = 8, alpha = 0.6)
    return plot!(legend = :none)
end

plot_distribution (generic function with 1 method)

num_of_type_0 = 250
num_of_type_1 = 250
neighborhood_size = 10 # Number of agents regarded as neighbors
preference = 0.5 # Want their kind to make at least this share of the neighborhood

# Create a list of agents
agents = vcat([Agent(kind = 0) for i in 1:num_of_type_0],
              [Agent(kind = 1) for i in 1:num_of_type_1])

plot_array = Any[]

# loop until none wishes to move
while true
    push!(plot_array, plot_distribution(agents))
    no_one_moved = true
    for agent in agents
        old_location = copy(agent.location)
        update!(agent)
        if norm(old_location - agent.location) ≉ 0
            no_one_moved = false
        end
    end
    if no_one_moved
        break
    end
end
n = length(plot_array)
plot(plot_array...,
     layout = (n, 1),
     size = (600, 400n),
     title = reshape(["Cycle $i" for i in 1:n], 1, n))

46. Schelling’s Segregation Model#

46.1. Overview#

46.2. The Model#