27. Shortest Paths#
Contents
27.1. Overview#
The shortest path problem is a classic problem in mathematics and computer science with applications in
Economics (sequential decision making, analysis of social networks, etc.)
Operations research and transportation
Robotics and artificial intelligence
Telecommunication network design and routing
etc., etc.
Variations of the methods we discuss in this lecture are used millions of times every day, in applications such as
Google Maps
routing packets on the internet
For us, the shortest path problem also provides a nice introduction to the logic of dynamic programming.
Dynamic programming is an extremely powerful optimization technique that we apply in many lectures on this site.
27.2. Outline of the Problem#
The shortest path problem is one of finding how to traverse a graph from one specified node to another at minimum cost.
Consider the following graph
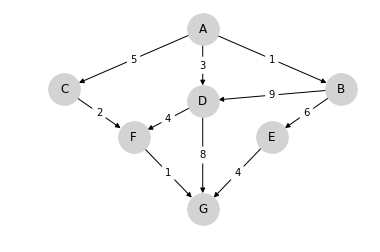
We wish to travel from node (vertex) A to node G at minimum cost.
Arrows (edges) indicate the movements we can take.
Numbers on edges indicate the cost of traveling that edge.
Possible interpretations of the graph include
Minimum cost for supplier to reach a destination.
Routing of packets on the internet (minimize time).
Etc., etc.
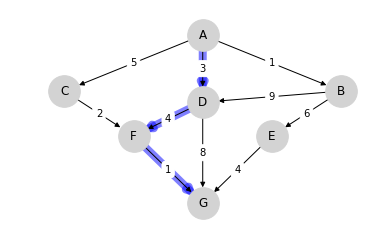
For this simple graph, a quick scan of the edges shows that the optimal paths are
A, C, F, G at cost 8
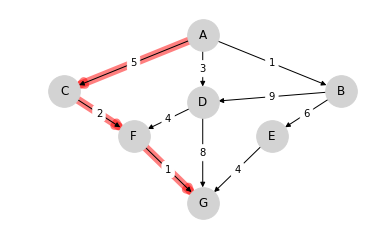
A, D, F, G at cost 8
27.3. Finding Least-Cost Paths#
For large graphs we need a systematic solution.
Let \(J(v)\) denote the minimum cost-to-go from node \(v\), understood as the total cost from \(v\) if we take the best route.
Suppose that we know \(J(v)\) for each node \(v\), as shown below for the graph from the preceding example
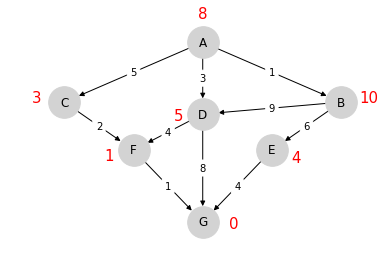
Note that \(J(G) = 0\).
The best path can now be found as follows
Start at A.
From node v, move to any node that solves
where
\(F_v\) is the set of nodes that can be reached from \(v\) in one step
\(c(v, w)\) is the cost of traveling from \(v\) to \(w\)
Hence, if we know the function \(J\), then finding the best path is almost trivial.
But how to find \(J\)?
Some thought will convince you that, for every node \(v\), the function \(J\) satisfies
This is known as the Bellman equation, after the mathematician Richard Bellman.
27.4. Solving for \(J\)#
The standard algorithm for finding \(J\) is to start with
where \(M\) is some large number.
Now we use the following algorithm
Set \(n = 0\).
Set \(J_{n+1} (v) = \min_{w \in F_v} \{ c(v, w) + J_n(w) \}\) for all \(v\).
If \(J_{n+1}\) and \(J_n\) are not equal then increment \(n\), go to 2.
In general, this sequence converges to \(J\)—the proof is omitted.
27.5. Exercises#
27.5.1. Exercise 1#
Use the algorithm given above to find the optimal path (and its cost) for the following graph.
using LinearAlgebra, Statistics
graph = Dict(zip(0:99,
[
[(14, 72.21), (8, 11.11), (1, 0.04)],
[(13, 64.94), (6, 20.59), (46, 1247.25)],
[(45, 1561.45), (31, 166.8), (66, 54.18)],
[(11, 42.43), (6, 2.06), (20, 133.65)],
[(7, 1.02), (5, 0.73), (75, 3706.67)],
[(11, 34.54), (7, 3.33), (45, 1382.97)],
[(10, 13.1), (9, 0.72), (31, 63.17)],
[(10, 5.85), (9, 3.15), (50, 478.14)],
[(12, 3.18), (11, 7.45), (69, 577.91)],
[(20, 16.53), (13, 4.42), (70, 2454.28)],
[(16, 25.16), (12, 1.87), (89, 5352.79)],
[(20, 65.08), (18, 37.55), (94, 4961.32)],
[(28, 170.04), (24, 34.32), (84, 3914.62)],
[(40, 475.33), (38, 236.33), (60, 2135.95)],
[(24, 38.65), (16, 2.7), (67, 1878.96)],
[(18, 2.57), (17, 1.01), (91, 3597.11)],
[(38, 278.71), (19, 3.49), (36, 392.92)],
[(23, 26.45), (22, 24.78), (76, 783.29)],
[(28, 55.84), (23, 16.23), (91, 3363.17)],
[(28, 70.54), (20, 0.24), (26, 20.09)],
[(33, 145.8), (24, 9.81), (98, 3523.33)],
[(31, 27.06), (28, 36.65), (56, 626.04)],
[(40, 124.22), (39, 136.32), (72, 1447.22)],
[(33, 22.37), (26, 2.66), (52, 336.73)],
[(28, 14.25), (26, 1.8), (66, 875.19)],
[(35, 45.55), (32, 36.58), (70, 1343.63)],
[(42, 122.0), (27, 0.01), (47, 135.78)],
[(43, 246.24), (35, 48.1), (65, 480.55)],
[(36, 15.52), (34, 21.79), (82, 2538.18)],
[(33, 12.61), (32, 4.22), (64, 635.52)],
[(35, 13.95), (33, 5.61), (98, 2616.03)],
[(44, 125.88), (36, 20.44), (98, 3350.98)],
[(35, 1.46), (34, 3.33), (97, 2613.92)],
[(47, 111.54), (41, 3.23), (81, 1854.73)],
[(48, 129.45), (42, 51.52), (73, 1075.38)],
[(50, 78.81), (41, 2.09), (52, 17.57)],
[(57, 260.46), (54, 101.08), (71, 1171.6)],
[(46, 80.49), (38, 0.36), (75, 269.97)],
[(42, 8.78), (40, 1.79), (93, 2767.85)],
[(41, 1.34), (40, 0.95), (50, 39.88)],
[(54, 53.46), (47, 28.57), (75, 548.68)],
[(54, 162.24), (46, 0.28), (53, 18.23)],
[(72, 437.49), (47, 10.08), (59, 141.86)],
[(60, 116.23), (54, 95.06), (98, 2984.83)],
[(47, 2.14), (46, 1.56), (91, 807.39)],
[(49, 15.51), (47, 3.68), (58, 79.93)],
[(67, 65.48), (57, 27.5), (52, 22.68)],
[(61, 172.64), (56, 49.31), (50, 2.82)],
[(60, 66.44), (59, 34.52), (99, 2564.12)],
[(56, 10.89), (50, 0.51), (78, 53.79)],
[(55, 20.1), (53, 1.38), (85, 251.76)],
[(60, 73.79), (59, 23.67), (98, 2110.67)],
[(66, 123.03), (64, 102.41), (94, 1471.8)],
[(67, 88.35), (56, 4.33), (72, 22.85)],
[(73, 238.61), (59, 24.3), (88, 967.59)],
[(64, 60.8), (57, 2.13), (84, 86.09)],
[(61, 11.06), (57, 0.02), (76, 197.03)],
[(60, 7.01), (58, 0.46), (86, 701.09)],
[(65, 34.32), (64, 29.85), (83, 556.7)],
[(71, 0.67), (60, 0.72), (90, 820.66)],
[(67, 1.63), (65, 4.76), (76, 48.03)],
[(64, 4.88), (63, 0.95), (98, 1057.59)],
[(76, 38.43), (64, 2.94), (91, 132.23)],
[(75, 56.34), (72, 70.08), (66, 4.43)],
[(76, 11.98), (65, 0.3), (80, 47.73)],
[(73, 33.23), (66, 0.64), (94, 594.93)],
[(73, 37.53), (68, 2.66), (98, 395.63)],
[(70, 0.98), (68, 0.09), (82, 153.53)],
[(71, 1.66), (70, 3.35), (94, 232.1)],
[(73, 8.99), (70, 0.06), (99, 247.8)],
[(73, 8.37), (72, 1.5), (76, 27.18)],
[(91, 284.64), (74, 8.86), (89, 104.5)],
[(92, 133.06), (84, 102.77), (76, 15.32)],
[(90, 243.0), (76, 1.4), (83, 52.22)],
[(78, 8.08), (76, 0.52), (81, 1.07)],
[(77, 1.19), (76, 0.81), (92, 68.53)],
[(78, 2.36), (77, 0.45), (85, 13.18)],
[(86, 64.32), (78, 0.98), (80, 8.94)],
[(81, 2.59), (98, 355.9)],
[(91, 22.35), (85, 1.45), (81, 0.09)],
[(98, 264.34), (88, 28.78), (92, 121.87)],
[(92, 99.89), (89, 39.52), (94, 99.78)],
[(93, 11.99), (88, 28.05), (91, 47.44)],
[(88, 5.78), (86, 8.75), (94, 114.95)],
[(98, 121.05), (94, 30.41), (89, 19.14)],
[(89, 4.9), (87, 2.66), (97, 94.51)],
[(97, 85.09)],
[(92, 21.23), (91, 11.14), (88, 0.21)],
[(98, 6.12), (91, 6.83), (93, 1.31)],
[(99, 82.12), (97, 36.97)],
[(99, 50.99), (94, 10.47), (96, 23.53)],
[(97, 22.17)],
[(99, 34.68), (97, 11.24), (96, 10.83)],
[(99, 32.77), (97, 6.71), (94, 0.19)],
[(96, 2.03), (98, 5.91)],
[(99, 0.27), (98, 6.17)],
[(99, 5.87), (97, 0.43), (98, 3.32)],
[(98, 0.3)],
[(99, 0.33)],
[(99, 0.0)],
]))
Dict{Int64, Vector{Tuple{Int64, Float64}}} with 100 entries:
5 => [(11, 34.54), (7, 3.33), (45, 1382.97)]
56 => [(61, 11.06), (57, 0.02), (76, 197.03)]
35 => [(50, 78.81), (41, 2.09), (52, 17.57)]
55 => [(64, 60.8), (57, 2.13), (84, 86.09)]
60 => [(67, 1.63), (65, 4.76), (76, 48.03)]
30 => [(35, 13.95), (33, 5.61), (98, 2616.03)]
32 => [(35, 1.46), (34, 3.33), (97, 2613.92)]
6 => [(10, 13.1), (9, 0.72), (31, 63.17)]
67 => [(70, 0.98), (68, 0.09), (82, 153.53)]
45 => [(49, 15.51), (47, 3.68), (58, 79.93)]
73 => [(90, 243.0), (76, 1.4), (83, 52.22)]
64 => [(76, 11.98), (65, 0.3), (80, 47.73)]
90 => [(99, 50.99), (94, 10.47), (96, 23.53)]
4 => [(7, 1.02), (5, 0.73), (75, 3706.67)]
13 => [(40, 475.33), (38, 236.33), (60, 2135.95)]
54 => [(73, 238.61), (59, 24.3), (88, 967.59)]
63 => [(75, 56.34), (72, 70.08), (66, 4.43)]
86 => [(97, 85.09)]
91 => [(97, 22.17)]
62 => [(76, 38.43), (64, 2.94), (91, 132.23)]
58 => [(65, 34.32), (64, 29.85), (83, 556.7)]
52 => [(66, 123.03), (64, 102.41), (94, 1471.8)]
12 => [(28, 170.04), (24, 34.32), (84, 3914.62)]
28 => [(36, 15.52), (34, 21.79), (82, 2538.18)]
75 => [(77, 1.19), (76, 0.81), (92, 68.53)]
⋮ => ⋮
The cost from node 68 to node 71 is 1.66 and so on.
27.6. Solutions#
27.6.1. Exercise 1#
function update_J!(J, graph)
next_J = Dict()
for node in keys(graph)
if node == 99
next_J[node] = 0
else
next_J[node] = minimum(cost + J[dest] for (dest, cost) in graph[node])
end
end
return next_J
end
function print_best_path(J, graph)
sum_costs = 0.0
current_location, destination = extrema(keys(graph))
while current_location != destination
println("node $current_location")
running_min = 1e10
minimizer_dest = Inf
minimizer_cost = 1e10
for (dest, cost) in graph[current_location]
cost_of_path = cost + J[dest]
if cost_of_path < running_min
running_min = cost_of_path
minimizer_cost = cost
minimizer_dest = dest
end
end
current_location = minimizer_dest
sum_costs += minimizer_cost
end
sum_costs = round(sum_costs, digits = 2)
println("node $destination\nCost: $sum_costs")
end
J = Dict((node => Inf) for node in keys(graph))
while true
next_J = update_J!(J, graph)
if next_J == J
break
else
J = next_J
end
end
print_best_path(J, graph)
node 0
node 8
node 11
node 18
node 23
node 33
node 41
node 53
node 56
node 57
node 60
node 67
node 70
node 73
node 76
node 85
node 87
node 88
node 93
node 94
node 96
node 97
node 98
node 99
Cost: 160.55