9. Solvers, Optimizers, and Automatic Differentiation#
Contents
9.1. Overview#
In this lecture we introduce a few of the Julia libraries that we’ve found particularly useful for quantitative work in economics.
using LinearAlgebra, Statistics
using ForwardDiff, Optim, JuMP, Ipopt, Roots, NLsolve
using Optim: converged, maximum, maximizer, minimizer, iterations #some extra functions
9.2. Introduction to Differentiable Programming#
The promise of differentiable programming is that we can move towards taking the derivatives of almost arbitrarily complicated computer programs, rather than simply thinking about the derivatives of mathematical functions. Differentiable programming is the natural evolution of automatic differentiation (AD, sometimes called algorithmic differentiation).
Stepping back, there are three ways to calculate the gradient or Jacobian
Analytic derivatives / Symbolic differentiation
You can sometimes calculate the derivative on pen-and-paper, and potentially simplify the expression.
In effect, repeated applications of the chain rule, product rule, etc.
It is sometimes, though not always, the most accurate and fastest option if there are algebraic simplifications.
Sometimes symbolic integration on the computer a good solution, if the package can handle your functions. Doing algebra by hand is tedious and error-prone, but is sometimes invaluable.
Finite differences
Evaluate the function at least \(N+1\) times to get the gradient – Jacobians are even worse.
Large \(\Delta\) is numerically stable but inaccurate, too small of \(\Delta\) is numerically unstable but more accurate.
Choosing the \(\Delta\) is hard, so use packages such as DiffEqDiffTools.jl.
If a function is \(R^N \to R\) for a large \(N\), this requires \(O(N)\) function evaluations.
Automatic Differentiation
The same as analytic/symbolic differentiation, but where the chain rule is calculated numerically rather than symbolically.
Just as with analytic derivatives, can establish rules for the derivatives of individual functions (e.g. \(d\left(sin(x)\right)\) to \(cos(x) dx\)) for intrinsic derivatives.
AD has two basic approaches, which are variations on the order of evaluating the chain rule: reverse and forward mode (although mixed mode is possible).
If a function is \(R^N \to R\), then reverse-mode AD can find the gradient in \(O(1)\) sweep (where a “sweep” is \(O(1)\) function evaluations).
If a function is \(R \to R^N\), then forward-mode AD can find the jacobian in \(O(1)\) sweeps.
We will explore two types of automatic differentiation in Julia (and discuss a few packages which implement them). For both, remember the chain rule
Forward-mode starts the calculation from the left with \(\frac{dy}{dw}\) first, which then calculates the product with \(\frac{dw}{dx}\). On the other hand, reverse mode starts on the right hand side with \(\frac{dw}{dx}\) and works backwards.
Take an example a function with fundamental operations and known analytical derivatives
And rewrite this as a function which contains a sequence of simple operations and temporaries.
function f(x_1, x_2)
w_1 = x_1
w_2 = x_2
w_3 = w_1 * w_2
w_4 = sin(w_1)
w_5 = w_3 + w_4
return w_5
end
f (generic function with 1 method)
Here we can identify all of the underlying functions (*, sin, +), and see if each has an
intrinsic derivative. While these are obvious, with Julia we could come up with all sorts of differentiation rules for arbitrarily
complicated combinations and compositions of intrinsic operations. In fact, there is even a package for registering more.
9.2.1. Forward-Mode Automatic Differentiation#
In forward-mode AD, you first fix the variable you are interested in (called “seeding”), and then evaluate the chain rule in left-to-right order.
For example, with our \(f(x_1, x_2)\) example above, if we wanted to calculate the derivative with respect to \(x_1\) then we can seed the setup accordingly. \(\frac{\partial w_1}{\partial x_1} = 1\) since we are taking the derivative of it, while \(\frac{\partial w_2}{\partial x_1} = 0\).
Following through with these, redo all of the calculations for the derivative in parallel with the function itself.
Since these two could be done at the same time, we say there is “one pass” required for this calculation.
Generalizing a little, if the function was vector-valued, then that single pass would get the entire row of the Jacobian in that single pass. Hence for a \(R^N \to R^M\) function, requires \(N\) passes to get a dense Jacobian using forward-mode AD.
How can you implement forward-mode AD? It turns out to be fairly easy with a generic programming language to make a simple example (while the devil is in the details for a high-performance implementation).
9.2.2. Forward-Mode with Dual Numbers#
One way to implement forward-mode AD is to use dual numbers.
Instead of working with just a real number, e.g. \(x\), we will augment each with an infinitesimal \(\epsilon\) and use \(x + \epsilon\).
From Taylor’s theorem,
where we will define the infinitesimal such that \(\epsilon^2 = 0\).
With this definition, we can write a general rule for differentiation of \(g(x,y)\) as the chain rule for the total derivative
But, note that if we keep track of the constant in front of the \(\epsilon\) terms (e.g. a \(x'\) and \(y'\))
This is simply the chain rule. A few more examples
Using the generic programming in Julia, it is easy to define a new dual number type which can encapsulate the pair \((x, x')\) and provide a definitions for all of the basic operations. Each definition then has the chain-rule built into it.
With this approach, the “seed” process is simple the creation of the \(\epsilon\) for the underlying variable.
So if we have the function \(f(x_1, x_2)\) and we wanted to find the derivative \(\partial_{x_1} f(3.8, 6.9)\) then then we would seed them with the dual numbers \(x_1 \to (3.8, 1)\) and \(x_2 \to (6.9, 0)\).
If you then follow all of the same scalar operations above with a seeded dual number, it will calculate both the function value and the derivative in a single “sweep” and without modifying any of your (generic) code.
9.2.3. ForwardDiff.jl#
Dual-numbers are at the heart of one of the AD packages we have already seen.
using ForwardDiff
h(x) = sin(x[1]) + x[1] * x[2] + sinh(x[1] * x[2]) # multivariate.
x = [1.4 2.2]
@show ForwardDiff.gradient(h, x) # use AD, seeds from x
#Or, can use complicated functions of many variables
f(x) = sum(sin, x) + prod(tan, x) * sum(sqrt, x)
g = (x) -> ForwardDiff.gradient(f, x); # g() is now the gradient
g(rand(5)) # gradient at a random point
# ForwardDiff.hessian(f,x') # or the hessian
ForwardDiff.gradient(h, x) = [26.35476496103098 16.663053156992287]
5-element Vector{Float64}:
1.7287884984367046
1.617599609299567
1.662997682902127
1.5950093906546172
3.724116399099141
We can even auto-differentiate complicated functions with embedded iterations.
function squareroot(x) #pretending we don't know sqrt()
z = copy(x) # Initial starting point for Newton’s method
while abs(z * z - x) > 1e-13
z = z - (z * z - x) / (2z)
end
return z
end
squareroot(2.0)
1.4142135623730951
using ForwardDiff
dsqrt(x) = ForwardDiff.derivative(squareroot, x)
dsqrt(2.0)
0.35355339059327373
9.2.4. Reverse-Mode AD#
Unlike forward-mode auto-differentiation, reverse-mode is very difficult to implement efficiently, and there are many variations on the best approach.
Many reverse-mode packages are connected to machine-learning packages, since the efficient gradients of \(R^N \to R\) loss functions are necessary for the gradient descent optimization algorithms used in machine learning.
At this point, Julia does not have a single consistently usable reverse-mode AD package without rough edges, but a few key ones to consider are:
ReverseDiff.jl, a relatively dependable but limited package. Not really intended for standard ML-pipline usage
Zygote.jl, which is flexible but buggy and less reliable. In a slow process of deprecation, but often the primary alternative.
Enzyme.jl, which is the most promising (and supports both forward and reverse mode). However, the usage is more tailored for scientific machine learning and scalar functions rather than fast GPU kernels, and it relies on a innovative (but not fully stable) approach to compilation.
9.3. Optimization#
There are a large number of packages intended to be used for optimization in Julia.
Part of the reason for the diversity of options is that Julia makes it possible to efficiently implement a large number of variations on optimization routines.
The other reason is that different types of optimization problems require different algorithms.
9.3.1. Optim.jl#
A good pure-Julia solution for the (unconstrained or box-bounded) optimization of univariate and multivariate function is the Optim.jl package.
By default, the algorithms in Optim.jl target minimization rather than
maximization, so if a function is called optimize it will mean minimization.
9.3.1.1. Univariate Functions on Bounded Intervals#
Univariate optimization defaults to a robust hybrid optimization routine called Brent’s method.
using Optim
using Optim: converged, maximum, maximizer, minimizer, iterations #some extra functions
result = optimize(x -> x^2, -2.0, 1.0)
Results of Optimization Algorithm
* Status: success
* Algorithm: Brent's Method
* Search Interval: [-2.000000, 1.000000]
* Minimizer: 0.000000e+00
* Minimum: 0.000000e+00
* Iterations: 5
* Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true
* Objective Function Calls: 6
Always check if the results converged, and throw errors otherwise
converged(result) || error("Failed to converge in $(iterations(result)) iterations")
xmin = result.minimizer
result.minimum
0.0
The first line is a logical OR between converged(result) and error("...").
If the convergence check passes, the logical sentence is true, and it will proceed to the next line; if not, it will throw the error.
Or to maximize
f(x) = -x^2
result = maximize(f, -2.0, 1.0)
converged(result) || error("Failed to converge in $(iterations(result)) iterations")
xmin = maximizer(result)
fmax = maximum(result)
-0.0
Note: Notice that we call optimize results using result.minimizer, and maximize results using maximizer(result).
9.3.1.2. Unconstrained Multivariate Optimization#
There are a variety of algorithms and options for multivariate optimization.
From the documentation, the simplest version is
f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
x_iv = [0.0, 0.0]
results = optimize(f, x_iv) # i.e. optimize(f, x_iv, NelderMead())
* Status: success
* Candidate solution
Final objective value: 3.525527e-09
* Found with
Algorithm: Nelder-Mead
* Convergence measures
√(Σ(yᵢ-ȳ)²)/n ≤ 1.0e-08
* Work counters
Seconds run: 0 (vs limit Inf)
Iterations: 60
f(x) calls: 117
The default algorithm in NelderMead, which is derivative-free and hence requires many function evaluations.
To change the algorithm type to L-BFGS
results = optimize(f, x_iv, LBFGS())
println("minimum = $(results.minimum) with argmin = $(results.minimizer) in " *
"$(results.iterations) iterations")
minimum = 5.378388330692143e-17 with argmin = [0.9999999926662504, 0.9999999853325008] in 24 iterations
Note that this has fewer iterations.
As no derivative was given, it used finite differences to approximate the gradient of f(x).
However, since most of the algorithms require derivatives, you will often want to use auto differentiation or pass analytical gradients if possible.
f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
x_iv = [0.0, 0.0]
results = optimize(f, x_iv, LBFGS(), autodiff = :forward) # i.e. use ForwardDiff.jl
println("minimum = $(results.minimum) with argmin = $(results.minimizer) in " *
"$(results.iterations) iterations")
minimum = 5.191703158437428e-27 with argmin = [0.999999999999928, 0.9999999999998559] in 24 iterations
Note that we did not need to use ForwardDiff.jl directly, as long as our f(x) function was written to be generic (see the generic programming lecture ).
Alternatively, with an analytical gradient
f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
x_iv = [0.0, 0.0]
function g!(G, x)
G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1]
G[2] = 200.0 * (x[2] - x[1]^2)
end
results = optimize(f, g!, x_iv, LBFGS()) # or ConjugateGradient()
println("minimum = $(results.minimum) with argmin = $(results.minimizer) in " *
"$(results.iterations) iterations")
minimum = 5.191703158437428e-27 with argmin = [0.999999999999928, 0.9999999999998559] in 24 iterations
For derivative-free methods, you can change the algorithm – and have no need to provide a gradient
f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
x_iv = [0.0, 0.0]
results = optimize(f, x_iv, SimulatedAnnealing()) # or ParticleSwarm() or NelderMead()
* Status: failure (reached maximum number of iterations)
* Candidate solution
Final objective value: 3.606663e-04
* Found with
Algorithm: Simulated Annealing
* Convergence measures
|x - x'| = NaN ≰ 0.0e+00
|x - x'|/|x'| = NaN ≰ 0.0e+00
|f(x) - f(x')| = NaN ≰ 0.0e+00
|f(x) - f(x')|/|f(x')| = NaN ≰ 0.0e+00
|g(x)| = NaN ≰ 1.0e-08
* Work counters
Seconds run: 0 (vs limit Inf)
Iterations: 1000
f(x) calls: 1001
However, you will note that this did not converge, as stochastic methods typically require many more iterations as a tradeoff for their global-convergence properties.
See the maximum likelihood example and the accompanying Jupyter notebook.
9.3.2. JuMP.jl#
The JuMP.jl package is an ambitious implementation of a modelling language for optimization problems in Julia.
In that sense, it is more like an AMPL (or Pyomo) built on top of the Julia language with macros, and able to use a variety of different commerical and open source solvers.
If you have a linear, quadratic, conic, mixed-integer linear, etc. problem then this will likely be the ideal “meta-package” for calling various solvers.
For nonlinear problems, the modelling language may make things difficult for complicated functions (as it is not designed to be used as a general-purpose nonlinear optimizer).
See the quick start guide for more details on all of the options.
The following is an example of calling a linear objective with a nonlinear constraint (provided by an external function).
Here Ipopt stands for Interior Point OPTimizer, a nonlinear solver in Julia
using JuMP, Ipopt
# solve
# max( x[1] + x[2] )
# st sqrt(x[1]^2 + x[2]^2) <= 1
function squareroot(x) # pretending we don't know sqrt()
z = x # Initial starting point for Newton’s method
while abs(z * z - x) > 1e-13
z = z - (z * z - x) / (2z)
end
return z
end
m = Model(Ipopt.Optimizer)
# need to register user defined functions for AD
JuMP.register(m, :squareroot, 1, squareroot, autodiff = true)
@variable(m, x[1:2], start=0.5) # start is the initial condition
@objective(m, Max, sum(x))
@NLconstraint(m, squareroot(x[1]^2 + x[2]^2)<=1)
@show JuMP.optimize!(m)
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit https://github.com/coin-or/Ipopt
******************************************************************************
This is Ipopt version 3.14.16, running with linear solver MUMPS 5.7.3.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 0.00e+00 2.07e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.4100714e+00 0.00e+00 5.48e-02 -1.7 3.94e-01 - 1.00e+00 7.36e-01f 1
2 1.4113851e+00 0.00e+00 2.83e-08 -2.5 9.29e-04 - 1.00e+00 1.00e+00f 1
3 1.4140632e+00 0.00e+00 1.50e-09 -3.8 1.89e-03 - 1.00e+00 1.00e+00f 1
4 1.4142117e+00 0.00e+00 1.84e-11 -5.7 1.05e-04 - 1.00e+00 1.00e+00f 1
5 1.4142136e+00 0.00e+00 8.23e-09 -8.6 1.30e-06 - 1.00e+00 1.00e+00f 1
Number of Iterations....: 5
(scaled) (unscaled)
Objective...............: -1.4142135740093271e+00 1.4142135740093271e+00
Dual infeasibility......: 8.2280586788385790e-09 8.2280586788385790e-09
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Variable bound violation: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5059035815063646e-09 2.5059035815063646e-09
Overall NLP error.......: 8.2280586788385790e-09 8.2280586788385790e-09
Number of objective function evaluations = 6
Number of objective gradient evaluations = 6
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 6
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 6
Number of Lagrangian Hessian evaluations = 5
Total seconds in IPOPT = 1.629
EXIT: Optimal Solution Found.
JuMP.optimize!(m) = nothing
And this is an example of a quadratic objective
# solve
# min (1-x)^2 + (100(y-x^2)^2)
# st x + y >= 10
using JuMP, Ipopt
m = Model(Ipopt.Optimizer) # settings for the solver
@variable(m, x, start=0.0)
@variable(m, y, start=0.0)
@NLobjective(m, Min, (1 - x)^2+100(y - x^2)^2)
JuMP.optimize!(m)
println("x = ", value(x), " y = ", value(y))
# adding a (linear) constraint
@constraint(m, x + y==10)
JuMP.optimize!(m)
println("x = ", value(x), " y = ", value(y))
This is Ipopt version 3.14.16, running with linear solver MUMPS 5.7.3.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 0.00e+00 2.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 9.5312500e-01 0.00e+00 1.25e+01 -1.0 1.00e+00 - 1.00e+00 2.50e-01f 3
2 4.8320569e-01 0.00e+00 1.01e+00 -1.0 9.03e-02 - 1.00e+00 1.00e+00f 1
3 4.5708829e-01 0.00e+00 9.53e+00 -1.0 4.29e-01 - 1.00e+00 5.00e-01f 2
4 1.8894205e-01 0.00e+00 4.15e-01 -1.0 9.51e-02 - 1.00e+00 1.00e+00f 1
5 1.3918726e-01 0.00e+00 6.51e+00 -1.7 3.49e-01 - 1.00e+00 5.00e-01f 2
6 5.4940990e-02 0.00e+00 4.51e-01 -1.7 9.29e-02 - 1.00e+00 1.00e+00f 1
7 2.9144630e-02 0.00e+00 2.27e+00 -1.7 2.49e-01 - 1.00e+00 5.00e-01f 2
8 9.8586451e-03 0.00e+00 1.15e+00 -1.7 1.10e-01 - 1.00e+00 1.00e+00f 1
9 2.3237475e-03 0.00e+00 1.00e+00 -1.7 1.00e-01 - 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 2.3797236e-04 0.00e+00 2.19e-01 -1.7 5.09e-02 - 1.00e+00 1.00e+00f 1
11 4.9267371e-06 0.00e+00 5.95e-02 -1.7 2.53e-02 - 1.00e+00 1.00e+00f 1
12 2.8189505e-09 0.00e+00 8.31e-04 -2.5 3.20e-03 - 1.00e+00 1.00e+00f 1
13 1.0095040e-15 0.00e+00 8.68e-07 -5.7 9.78e-05 - 1.00e+00 1.00e+00f 1
14 1.3288608e-28 0.00e+00 2.02e-13 -8.6 4.65e-08 - 1.00e+00 1.00e+00f 1
Number of Iterations....: 14
(scaled) (unscaled)
Objective...............: 1.3288608467480825e-28 1.3288608467480825e-28
Dual infeasibility......: 2.0183854587685121e-13 2.0183854587685121e-13
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Variable bound violation: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 0.0000000000000000e+00 0.0000000000000000e+00
Overall NLP error.......: 2.0183854587685121e-13 2.0183854587685121e-13
Number of objective function evaluations = 36
Number of objective gradient evaluations = 15
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 14
Total seconds in IPOPT = 0.026
EXIT: Optimal Solution Found.
x = 0.9999999999999899
y = 0.9999999999999792
This is Ipopt version 3.14.16, running with linear solver MUMPS 5.7.3.
Number of nonzeros in equality constraint Jacobian...: 2
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 1
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 1.00e+01 1.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 9.6315968e+05 1.78e-15 3.89e+05 -1.0 9.91e+00 - 1.00e+00 1.00e+00h 1
2 1.6901461e+05 0.00e+00 1.16e+05 -1.0 3.24e+00 - 1.00e+00 1.00e+00f 1
3 2.5433173e+04 0.00e+00 3.18e+04 -1.0 2.05e+00 - 1.00e+00 1.00e+00f 1
4 2.6527756e+03 0.00e+00 7.79e+03 -1.0 1.19e+00 - 1.00e+00 1.00e+00f 1
5 1.1380324e+02 0.00e+00 1.35e+03 -1.0 5.62e-01 - 1.00e+00 1.00e+00f 1
6 3.3745506e+00 0.00e+00 8.45e+01 -1.0 1.50e-01 - 1.00e+00 1.00e+00f 1
7 2.8946196e+00 0.00e+00 4.22e-01 -1.0 1.07e-02 - 1.00e+00 1.00e+00f 1
8 2.8946076e+00 0.00e+00 1.07e-05 -1.7 5.42e-05 - 1.00e+00 1.00e+00f 1
9 2.8946076e+00 0.00e+00 5.91e-13 -8.6 1.38e-09 - 1.00e+00 1.00e+00f 1
Number of Iterations....: 9
(scaled) (unscaled)
Objective...............: 2.8946075504894599e+00 2.8946075504894599e+00
Dual infeasibility......: 5.9130478291535837e-13 5.9130478291535837e-13
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Variable bound violation: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 0.0000000000000000e+00 0.0000000000000000e+00
Overall NLP error.......: 5.9130478291535837e-13 5.9130478291535837e-13
Number of objective function evaluations = 10
Number of objective gradient evaluations = 10
Number of equality constraint evaluations = 10
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 1
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 9
Total seconds in IPOPT = 0.003
EXIT: Optimal Solution Found.
x =
2.701147124098218 y = 7.2988528759017814
9.3.3. BlackBoxOptim.jl#
Another package for doing global optimization without derivatives is BlackBoxOptim.jl.
An example for parallel execution of the objective is provided.
9.4. Systems of Equations and Least Squares#
9.4.1. Roots.jl#
A root of a real function \(f\) on \([a,b]\) is an \(x \in [a, b]\) such that \(f(x)=0\).
For example, if we plot the function
with \(x \in [0,1]\) we get
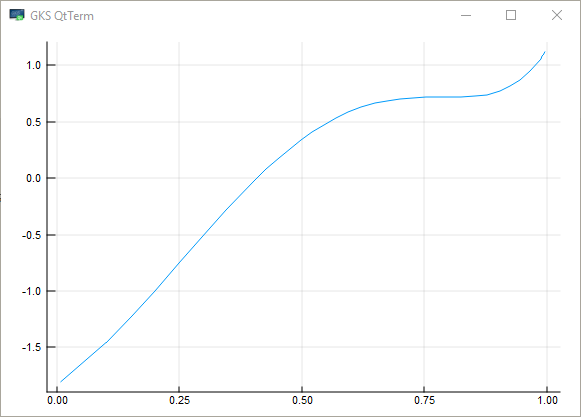
The unique root is approximately 0.408.
The Roots.jl package offers fzero() to find roots
using Roots
f(x) = sin(4 * (x - 1 / 4)) + x + x^20 - 1
fzero(f, 0, 1)
0.40829350427936706
9.4.2. NLsolve.jl#
The NLsolve.jl package provides functions to solve for multivariate systems of equations and fixed points.
From the documentation, to solve for a system of equations without providing a Jacobian
using NLsolve
f(x) = [(x[1] + 3) * (x[2]^3 - 7) + 18
sin(x[2] * exp(x[1]) - 1)] # returns an array
results = nlsolve(f, [0.1; 1.2])
Results of Nonlinear Solver Algorithm
* Algorithm: Trust-region with dogleg and autoscaling
* Starting Point: [0.1, 1.2]
* Zero: [-7.775548712324193e-17, 0.9999999999999999]
* Inf-norm of residuals: 0.000000
* Iterations: 4
* Convergence: true
* |x - x'| < 0.0e+00: false
* |f(x)| < 1.0e-08: true
* Function Calls (f): 5
* Jacobian Calls (df/dx): 5
In the above case, the algorithm used finite differences to calculate the Jacobian.
Alternatively, if f(x) is written generically, you can use auto-differentiation with a single setting.
results = nlsolve(f, [0.1; 1.2], autodiff = :forward)
println("converged=$(NLsolve.converged(results)) at root=$(results.zero) in " *
"$(results.iterations) iterations and $(results.f_calls) function calls")
converged=true at root=[-3.7818049096324184e-16, 1.0000000000000002] in 4 iterations and 5 function calls
Providing a function which operates inplace (i.e., modifies an argument) may help performance for large systems of equations (and hurt it for small ones).
function f!(F, x) # modifies the first argument
F[1] = (x[1] + 3) * (x[2]^3 - 7) + 18
F[2] = sin(x[2] * exp(x[1]) - 1)
end
results = nlsolve(f!, [0.1; 1.2], autodiff = :forward)
println("converged=$(NLsolve.converged(results)) at root=$(results.zero) in " *
"$(results.iterations) iterations and $(results.f_calls) function calls")
converged=true at root=[-3.7818049096324184e-16, 1.0000000000000002] in 4 iterations and 5 function calls
9.5. LeastSquaresOptim.jl#
Many optimization problems can be solved using linear or nonlinear least squares.
Let \(x \in R^N\) and \(F(x) : R^N \to R^M\) with \(M \geq N\), then the nonlinear least squares problem is
While \(F(x)^T F(x) \to R\), and hence this problem could technically use any nonlinear optimizer, it is useful to exploit the structure of the problem.
In particular, the Jacobian of \(F(x)\), can be used to approximate the Hessian of the objective.
As with most nonlinear optimization problems, the benefits will typically become evident only when analytical or automatic differentiation is possible.
If \(M = N\) and we know a root \(F(x^*) = 0\) to the system of equations exists, then NLS is the defacto method for solving large systems of equations.
An implementation of NLS is given in LeastSquaresOptim.jl.
9.6. Exercises#
9.6.1. Exercise 1#
Doing a simple implementation of forward-mode auto-differentiation is very easy in Julia since it is generic. In this exercise, you will fill in a few of the operations required for a simple AD implementation.
First, we need to provide a type to hold the dual.
struct DualNumber{T} <: Real
val::T
ϵ::T
end
Here we have made it a subtype of Real so that it can pass through functions expecting Reals.
We can add on a variety of chain rule definitions by importing in the appropriate functions and adding DualNumber versions. For example
import Base: +, *, -, ^, exp
+(x::DualNumber, y::DualNumber) = DualNumber(x.val + y.val, x.ϵ + y.ϵ) # dual addition
+(x::DualNumber, a::Number) = DualNumber(x.val + a, x.ϵ) # i.e. scalar addition, not dual
+(a::Number, x::DualNumber) = DualNumber(x.val + a, x.ϵ) # i.e. scalar addition, not dual
+ (generic function with 290 methods)
With that, we can seed a dual number and find simple derivatives,
f(x, y) = 3.0 + x + y
x = DualNumber(2.0, 1.0) # x -> 2.0 + 1.0\epsilon
y = DualNumber(3.0, 0.0) # i.e. y = 3.0, no derivative
# seeded calculates both teh function and the d/dx gradient!
f(x, y)
DualNumber{Float64}(8.0, 1.0)
For this assignment:
Add in AD rules for the other operations:
*, -, ^, exp.Come up with some examples of univariate and multivariate functions combining those operations and use your AD implementation to find the derivatives.